Semiprobabilistisches Sicherheitskonzept
Kurzdarstellung des semiprobabilistischen Sicherheitskonzeptes
- Anmerkung
Dieser Artikel enthält eine inhaltliche Kurzfassung der derzeit geltenden Europäischen Normenwerke sowie der derzeit geltenden Bemessungs- und Konstruktionsnorm für Holztragwerke in Deutschland
und erhebt naturgemäß keinen Anspruch auf Vollständigkeit. Es ersetzt im Anwendungsfall keinesfalls die detaillierten Festlegungen der jeweiligen Normen, welche in jedem Fall heranzuziehen und als
bindend zu betrachten sind.
Die redaktionelle Erarbeitung erfolgte im Hinblick auf die Darstellung der Eigenschaften vom SHERPA Holzverbinder-System.
Einführung
Der Holzbau hat sich durch die verschiedenen Baukulturen der Völker, den unterschiedlichen regionalen Holzarten und nicht zuletzt von den getrennt durchgeführten Holzforschungen und den damit verbundenen Erfahrungen, regional in sehr unterschiedlichen Bauweisen weiterentwickelt [1]. Durch die Europäisierung und dem damit einhergehenden Wunsch Handelshemmnisse abzubauen, wurde ab den 70er-Jahren mit der Harmonisierung nationaler Regelungen begonnen [1]. Mit der Normenserie EN 1995-1-1:2004/A1:2008 [N 1] und EN 1995-1-2:2006 stehen dem Holzbau heute Dokumente zur Verfügung, die durch gesichertes Fachwissen eine auf europäischer Ebene einheitliche Bemessung von Holzbauten ermöglichen [1]. Damit den regionalen Bedürfnissen und Anforderungen der Länder nachgekommen werden kann, erfolgte eine Erweiterung der Grundlagendokumente der Eurocodes durch nationale Anhänge. Für die Anwendung des Eurocode 5 EN 1995-1-1:2004/A1:2008 [N 1] sind gewisse Vorkenntnisse nötig, damit ein sicherer Umgang mit den semi-probabilistischen Bemessungskonzepten erfolgen kann.
In Deutschland findet durch die DIN 1052:2008 [N 2] dasselbe Sicherheitskonzept Anwendung, weshalb es unter anderem noch zu keiner vollständigen Umstellung auf den Eurocode 5 gekommen ist. Da mit der DIN 1052:2008 ein sehr gutes Normenwerk zur Verfügung steht, werden auch in anderen Ländern sehr häufig noch Bemessungsregeln daraus verwendet. Mit der Zeit wird es allerdings auch hierzu einer Angleichung kommen müssen.
Der SHERPA®-Verbinder mit der allgemeinen bauaufsichtlichen Zulassung Z-9.1-558 vom Deutschen Institut für Bautechnik (DIBt) unterliegt den Regeln der DIN 1052:2008. In den folgenden Punkten werden die Methoden der Berechnung von Holzbauwerken nach den semi-probabilistischen Sicherheitskonzepten der beiden Regelwerke DIN 1052:2008 und der EN 1995-1-1:2004/A1:2008 vorgestellt. Durch den Sitz der Vinzenz Harrer GmbH in Frohnleiten bei Graz, werden in bestimmten Punkten auch Angaben aus dem nationalen Anhang für Österreich ÖNORM B 1995-1-1:2009 [N 3] gemacht. Im Anschluss daran werden die Nachweise für die Grenzzustände der Tragfähigkeit und der Gebrauchstauglichkeit der EN 1995-1-1:2004/A1:2008 und der DIN 1052:2008 vorgestellt und auch miteinander verglichen.
Die gezeigten Rechenmodelle beinhalten nur einen kleinen Teil der beiden genannten Regelwerke und dürfen somit keinesfalls als Ersatz der jeweils gültigen Normendokumente verstanden werden.
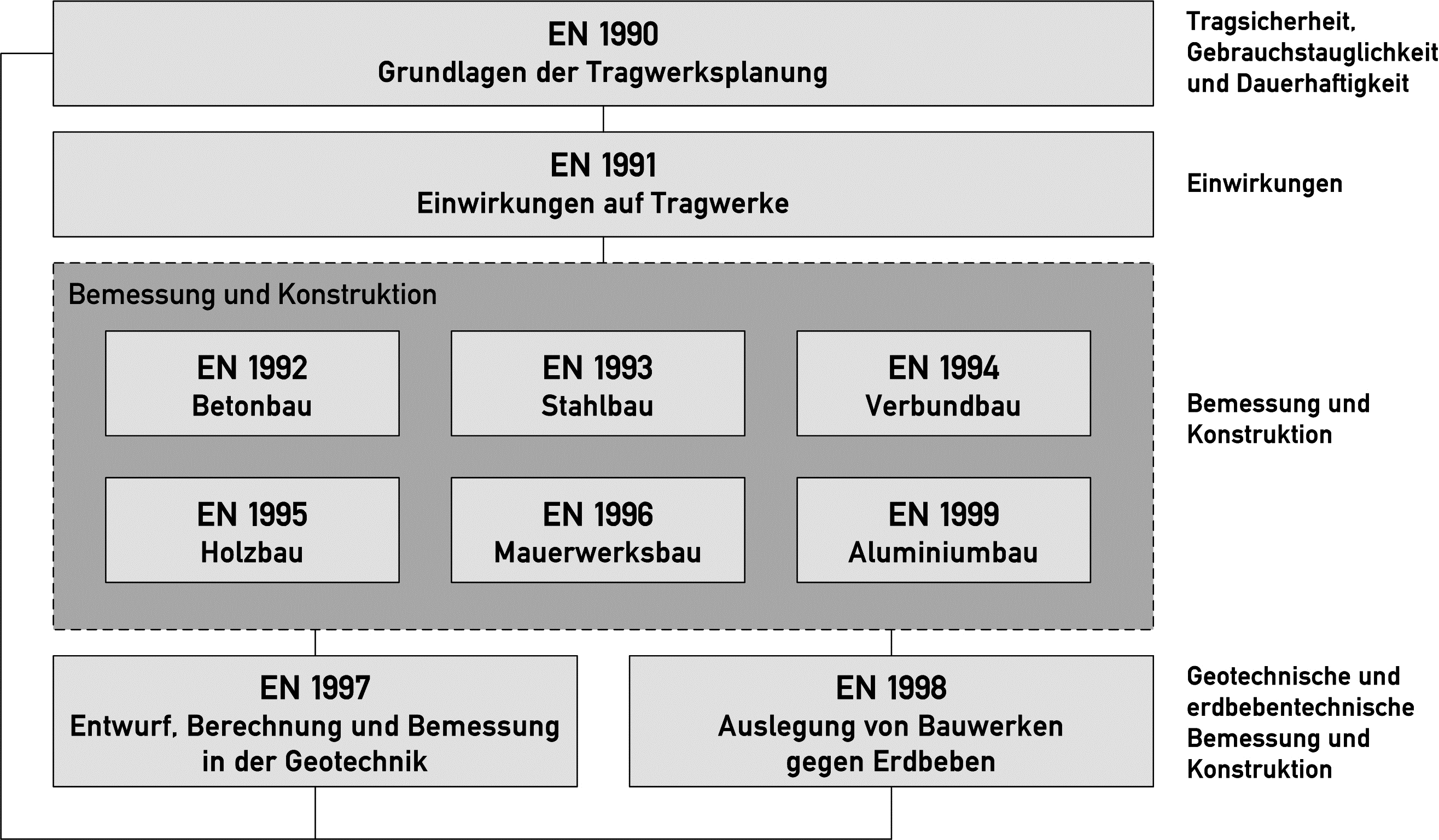
Viele Parameter in den Berechnungskonzepten zur Dimensionierung von Bauteilen unterliegen natürlichen statistischen Streuungen. Damit die in diesem Zusammenhang entstehenden Unsicherheiten der Modellannahmen quantifiziert und das Versagensrisiko so gering wie möglich gehalten und auch bewertet werden kann, werden in den Normenwerken die Berechnungskonzepte nach dem semi-probabilistischen Sicherheitskonzept aufgebaut. Die europäischen Normenwerke zur Bemessung von Tragwerken sind der Abb. 1.1 zu entnehmen.
Abb. 1.1: Europäische Normenwerke im Überblick [2]
Neben den Definitionen des Sicherheitskonzepts in
- EN 1990 Grundlagen der Tragwerksplanung
sind für den Bereich des konstruktiven Holzbaues die Normengruppe der Einwirkungen
- EN 1991 Einwirkungen auf Tragwerke
sowie die Bemessungs- und Konstruktionsnormengruppen
- EN 1995 Bemessung und Konstruktion von Holzbauten
- EN 1993 Bemessung und Konstruktion von Stahlbauten
- EN 1992 Bemessung und Konstruktion von Betonbauten
- EN 1998 Auslegung von Bauwerken gegen Erdbeben
von besonderer Relevanz.
Die Bemessung und Konstruktion von Holzbauten wird in Europa einheitlich durch die Normenwerke
| • EN 1995-1-1:2004/A1:2008 | Bemessung und Konstruktion von Holzbauten Teil 1-1: Allgemeines - Allgemeine Regeln und Regeln für den Hochbau | |
| • EN 1995-1-2:2006 | Bemessung und Konstruktion von Holzbauten Teil 1-2: Allgemeine Regeln - Bemessung für den Brandfall | |
| • EN 1995-2: 2006 | Bemessung und Konstruktion von Holzbauten Teil 2: Brücken |
Neben den angeführten „Grundlagendokumenten“ besteht für die jeweiligen nationalen Normeninstitute noch die Möglichkeit der Herausgabe von sog. „Nationalen Anhängen“, in denen nationale Festlegungen, Erläuterungen und Ergänzungen zu den Grundlagendokumenten definiert werden können.
All diese Dokumente (ÖNORM EN 199x und ÖNORM B 199x) sind als geschlossene Einheit anzuwenden, und das Vermischen mit anderen Normenserien (ÖNORM B 4xxx, ÖNORM ENV 199x) ist nicht zulässig.
1.2
Grundsätzliches zur Bemessung nach Grenzzuständen
Allgemeines
Die auf dem semi-probabilistischem Sicherheitskonzept basierende Normenfamilie der Eurocodes und einzelner nationaler Normen, wie zum Beispiel DIN 1052:2008 [N 2], definieren über Grenzzustände die konstruktive Zuverlässigkeit der Tragsicherheit, Gebrauchstauglichkeit und Dauerhaftigkeit von Tragwerken. Werden die Grenzzustände überschritten, können die an ein Tragwerk gestellten Anforderungen nicht mehr gesichert erfüllt werden.
Grenzzustände der Tragfähigkeit (engl.: Ultimate Limit State (ULS)) [1]
Grenzzustände der Tragfähigkeit sind Zustände, bei deren Überschreitung es zu einem Einsturz des Tragwerks oder anderen Formen des Versagens kommen kann.
Kennzeichen der Grenzzustände der Tragfähigkeit sind:
- Gleichgewichtsverlust des gesamten Tragwerkes oder einzelner Tragwerksteile
(Montagezustände berücksichtigen) - Stabilitätsverluste (besonders bei schlanken Bauteilen)
- Eintritt von Versagensmechanismen am Gesamtsystem oder einzelner Tragwerksteile
Grenzzustände der Gebrauchstauglichkeit (engl.: Serviceability Limit State (SLS)) [1]
Die Verformungen bzw. Durchbiegungen eines Tragwerkes infolge von Beanspruchungen sollen in definierten Grenzen gehalten werden, um mögliche Schäden (wie z. B. Rissbildungen) an Bauteilen, wie Decken, Fußboden, Trennwänden, Installationen, etc. zu vermeiden. Auch gilt es, die Anforderungen hinsichtlich der Benutzbarkeit (Durchbiegungen, Schwingungen) und des Erscheinungsbildes bzw. des Wohlbefindens der Nutzer zu erfüllen.
Nachweise durch die Methode der Teilsicherheitsbeiwerte
Das in den Eurocodes und der DIN 1052:2008 verankerte Sicherheitskonzept beruht - im Gegensatz zum deterministischen Sicherheitskonzept mit einem globalen Sicherheitsbeiwert („Verfahren mit zulässigen Spannungen“ [3]) - auf der Nachweisführung mit sogenannten Teilsicherheitsbeiwerten. Diese Sicherheitsfaktoren werden verwendet, um das Versagensrisiko einer Tragstruktur, mit den für die Berechnung verbundenen Modellannahmen, so niedrig wie möglich zu halten. Dabei ist zu zeigen, dass in allen maßgebenden Bemessungssituationen beim Ansatz der Bemessungswerte für Einwirkungen oder deren Auswirkungen, für die Tragwiderstände keiner der maßgebenden Grenzzustände überschritten wird. Ein Vorteil dieser Methode ist die eindeutige Trennung der wichtigsten Einflussfaktoren für die Bemessung von Tragwerken.
Zu den wichtigsten Einflussfaktoren gehören:
- Einwirkungen: Nutzlasten, Schnee, Wind, Temperaturen, . . .
- Baustoffeigenschaften: Festigkeiten, Steifigkeiten,. . .
- geometrische Größen: Abmessungen, Geometrien, . . .
All diese Einflussfaktoren sind Zufallsgrößen, die statistischen Streuungen unterliegen.
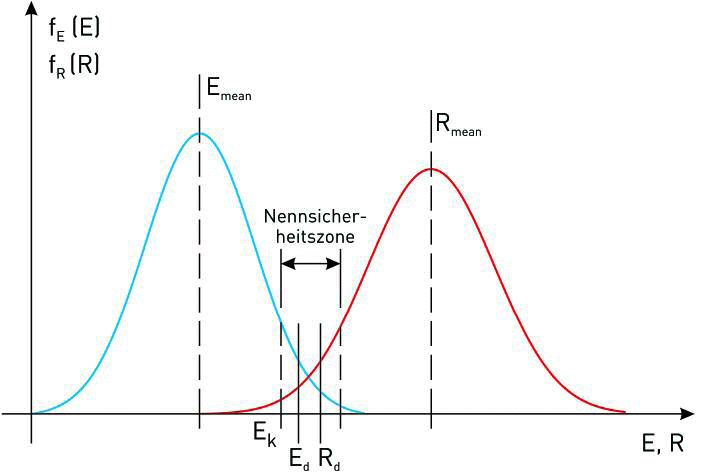
In Abb. 1.2 ist dieser Zusammenhang an Hand typischer Verteilungsfunktionen für die Einwirkung E und die Tragfähigkeit R eines Bauteils grafisch dargestellt. Beide Zufallskenngrößen weisen dabei streuenden Charakter auf. Ein Versagen lässt sich in dieser Darstellung durch den Zusammenhang R − E < 0 definieren. Für den Fall R − E = 0 wird dementsprechend gerade der Grenzzustand erreicht.
Auf Grund der Tatsache, dass für die beiden Verteilungsfunktionen — insbesondere an den Verteilungsenden — im Allgemeinen unzureichende empirische Kenntnisse vorliegen, begnügt man sich im Rahmen des semi-probabilistischen Sicherheitskonzeptes damit, dafür Sorge zu tragen, dass zwischen definierten Werten (charakteristischen Werten bzw. Bemessungswerten) der Verteilungsfunktionen ein ausreichender Sicherheitsabstand gewährleistet bleibt.
Durch das einheitliche Konzept der Eurocodes mit den Teilsicherheitsbeiwerten kann die Bemessung von Tragwerken baustoffunabhängig erfolgen und die Berechnungen für alle Baustoffe können auf denselben Konzepten basieren.
| Es bedeuten: | ||
| E | Einwirkung | |
| Emean | Mittelwert der Einwirkung | |
| Ek | Charakteristischer Wert der Einwirkung | |
| Ed | Bemessungswert der Einwirkung | |
| R | Widerstand | |
| Rmean | Mittelwert des Widerstandes | |
| Rk | Charakteristischer Wert des Widerstandes | |
| Rd | Bemessungswert des Widerstandes | |
Abb. 1.2: semi-probabilistisches Sicherheitskonzept
Auf Grund der zum Teil stark streuenden Eigenschaften des Roh- und Werkstoffes Holz hinsichtlich mechanischer Eigenschaften, des orthotropen (unterschiedliche Eigenschaften in Richtung der Längs-, Radial- und Tangentialachse) Material- und Feuchteverhaltens (Schwinden und Quellen in den genannten Richtungen) sowie der Inhomogenitäten in der Baustoffstruktur werden in Ergänzung zum semi-probabilistischen Sicherheitskonzept für die Bemessung und Konstruktion von Holztragwerken weitere Faktoren verwendet.
Diese ermöglichen unter anderem die Berücksichtigung unterschiedlicher Feuchtegehalte, der Dauer der Lasteinwirkung, die Verminderung der Querschnittsfläche infolge von Rissen oder auch des zeitabhängigen Verformungsverhaltens von Holzkonstruktionen.
1.3
Einwirkungen und Einwirkungskombinationen
Begriffe im Zusammenhang mit Einwirkungen
Unter Einwirkungen im Sinne des europäischen Normenkonzeptes versteht man übergeordnet:
- „eine Gruppe von Kräften (Lasten), die auf ein Tragwerk wirken (direkte Einwirkungen)“ (1.5.3.1 a)[N 4]),
sowie
- „eine Gruppe von aufgezwungenen Verformungen oder einer Beschleunigung, die z. B. durch Temperaturänderungen, Feuchtigkeitsänderung, ungleiche Setzung oder Erdbeben hervorgerufen werden (indirekte Einwirkungen) (1.5.3.1 b)[N 4]).
Die nachfolgende Abbildung enthält einen Überblick über die gegebenenfalls zu berücksichtigenden „Einwirkungsnormen“ nach EN 1991.
Abb. 1.3: EN-Normen zur Berücksichtigung der Einwirkungen [2]
Auswirkungen von Einwirkungen auf ein Tragwerk
Durch die Einwirkungen auf ein Tragwerk kommt es zu Beanspruchungen von Bauteilen (z. B. Schnittkräfte, Spannungen, Dehnungen) oder Reaktionen des Gesamttragwerks (z. B. Durchbiegungen, Verdrehungen).
Einteilung der Einwirkungen
- Ständige Einwirkungen (G) (1.5.3.3 [N 4])
Einwirkungen (direkte Einwirkungen wie z. B. das Eigengewicht von Konstruktionen, Gebäudeausrüstungen, ... , indirekte Auswirkungen wie Schwinden, ungleichmäßige Setzungen, ...), von denen vorausgesetzt wird, dass sie während der gesamten Nutzungsdauer in die gleiche Richtung wirken, und deren zeitliche Größenänderungen vernachlässigt werden können.
- veränderliche Einwirkungen (Q) (1.5.3.4 [N 4])
Einwirkungen (z. B. Nutzlasten auf Decken, Schneelasten, Windlasten), die nicht immer in die gleiche Richtung wirken und deren zeitliche Größenänderungen nicht vernachlässigbar sind.
- außergewöhnliche Einwirkungen (A) (1.5.3.5 [N 4])
Einwirkungen (z. B. Brand, Explosionen, Erdbeben, Fahrzeuganprall, ... ), die in der Regel von kurzer Dauer, aber von bedeutender Größenordnung sind und die während der geplanten Nutzungsdauer mit keiner nennenswerten Wahrscheinlichkeit auftreten können.
- Bemessungswert einer Einwirkung (Gd oder Qd) (1.5.3.21 [N 4])
Wert einer Einwirkung, der durch Multiplikation des repräsentativen Wertes mit dem Teilsicherheitsbeiwert ermittelt wird.
- Charakteristischer Wert einer Einwirkung (Gk oder Qk) (1.5.3.14 [N 4])
Wichtigster repräsentativer Wert einer Einwirkung.
Kombination von Einwirkungen (ohne Ermüdung)
Da Einwirkungen auf ein Tragwerk meistens in Kombinationen mit anderen (veränderlichen) Einwirkungen auftreten, müssen unterschiedliche Kombinationen mit der Berücksichtigung von Auftretenswahrscheinlichkeiten auf ein Tragwerk angesetzt werden.
Für die Bemessungssituationen wird unterschieden in
- ständige Situationen, die den üblichen Nutzungsbedingungen des Tragwerks entsprechen;
- vorübergehende Situationen, die sich auf zeitlich begrenzte Zustände des Tragwerks beziehen (Bauzustand, Instandsetzungen,. . . );
- außergewöhnliche Situation, die sich auf außergewöhnliche Bedingungen für das Tragwerk beziehen, z. B. Brand, Explosionen, Anprall oder Folgen lokalen Versagens;
- Situationen bei Erdbeben, die die Bedingungen bei Erdbebeneinwirkungen auf das Tragwerk umfassen [3].
„Die gewählten Bemessungssituationen müssen alle Bedingungen, die während der Ausführung und Nutzung des Tragwerks vernünftigerweise erwartet werden können, hinreichend genau erfassen“ (3.2 (3) [N 4]).
- Für die Kombinationsregeln gilt der allgemeine Grundsatz
Jede Einwirkungskombination sollte eine dominierende veränderliche Einwirkung (Leiteinwirkung mit einem Maximum) oder eine außergewöhnliche Einwirkung (Erdbeben, Fahrzeuganprall, ...) aufweisen. Die Auswirkungen der übrigen Einflüsse (Begleiteinwirkungen) sind, sofern aus physikalischen oder betrieblichen Gründen sinnvoll, zu berücksichtigen. Dabei soll jede veränderliche Einwirkung auch als Leiteinwirkung auftreten. Daraus lässt sich ableiten, dass die Anzahl der unterschiedlichen Lastfallkombinationen zumindest jener der unterschiedlichen voneinander unabhängigen veränderlichen Einwirkungen entspricht. Aus allen Kombinationen ist jene mit den ungünstigsten Auswirkungen auf das Tragverhalten der Struktur maßgebend. Die Integration der Einwirkungen erfolgt mit Hilfe von Teilsicherheitsbeiwerten γG und γQ und Kombinationsbeiwerten ψ .
Kombinationsregeln für Nachweise in den Grenzzuständen der Tragfähigkeit
Kombination von Einwirkungen bei ständigen (Normalsituationen) und vorübergehenden (Bausituationen) Bemessungssituationen (= Grundkombination) [N 4]
| (1.1) |
| mit | ||
| Ed | Bemessungswert einer Einwirkung | |
| ∑ | „gemeinsame Auswirkungen von“ (Summenbildung) | |
| ⊕ | „ist zu kombinieren“ | |
| Gk,j | Charakteristischer Wert der ständigen Einwirkung j | |
| γG,j | Teilsicherheitsbeiwert für die ständige Einwirkung j | |
| Qk,1 | Charakteristischer Wert der dominierenden veränderlichen Einwirkung | |
| γQ,1 | Teilsicherheitsbeiwert für die dominierende veränderliche Einwirkung | |
| Qk,i | Charakteristischer Wert der begleitenden veränderlichen Einwirkung i | |
| γQ,i | Teilsicherheitsbeiwert für die begleitende veränderliche Einwirkung i | |
| ψ | Kombinationsbeiwert einer veränderlichen Einwirkung |
Da das Aufstellen der Lastkombinationen mit einem relativ großen Rechenaufwand verbunden ist, werden in der DIN 1052:2008 [N 2] vereinfachte Regeln gemäß Gleichung (1.2) für die Anwendungen im Hochbau1 angegeben.
| (1.2) |
Anmerkung:
In der EN 1990 sind keine Vereinfachungen für die Einwirkungskombinationen zu finden.
Kombination von Einwirkungen bei außergewöhnlichen Bemessungssituationen (Brandfall, Explosionen, ...)[N 4]
| (1.3) |
| mit | ||
| Ed | Bemessungswert der Einwirkungskombination bei einer außergewöhnlichen Bemessungssituation | |
| Ad | Bemessungswert einer außergewöhnlichen Einwirkung | |
| ψ1,1 | Beiwert für häufige Werte der dominierenden veränderlichen Einwirkung | |
| ψ2,1 | Beiwert für quasi-ständige Werte der dominierenden veränderlichen Einwirkung | |
| ψ2,i | Beiwert für quasi-ständige Werte der begleitenden veränderlichen Einwirkungen |
Kombinationen von Einwirkungen für Bemessungssituation bei Erdbeben [N 4]
| (1.4) |
| mit | ||
| EdAE | Bemessungswert der Einwirkungskombination für die Bemessungssituation bei Erdbeben | |
| AEK | Charakteristischer Wert einer Einwirkung infolge Erdbeben | |
| γI | Wichtungsfaktor (siehe EN 1998) |
Kombinationsregeln für Nachweise in den Grenzzuständen der Gebrauchstauglichkeit
Die Kombinationen der Einwirkungen sollen an das Bauwerksverhalten und an die Nutzung des Gebäudes und den damit verbundenen Gebrauchstauglichkeitsanforderungen angepasst werden.
Allgemein ist die Bedingung nach [N 4]
| (1.5) |
zu erfüllen.
| mit | ||
| Ed | Bemessungswert der Einwirkungen auf Gebrauchstauglichkeitsniveau | |
| Cd | Bemessungswert der Grenze für das maßgebende Gebrauchstauglichkeitskriterium |
- Charakteristische Kombination [N 4]
Verwendung für nicht umkehrbare Auswirkungen auf ein Tragwerk
| (1.6) |
- Häufige Kombination [N 4]
Verwendung für umkehrbare Auswirkungen auf ein Tragwerk
| (1.7) |
- Quasi-ständige Kombination [N 4]
Verwendung für Langzeitauswirkungen (z. B. Erscheinungsbild) auf ein Tragwerk
| (1.8) |
Teilsicherheitsbeiwerte für Einwirkungen
Mit Hilfe der Teilsicherheitsbeiwerte werden die Modellunsicherheiten und Größenabweichungen der Einwirkungen und deren Auswirkungen berücksichtigt.
| Grenzustände der Tragfähigkeit für Nachweise der Lagesicherheit (EQU) und der Tragfähigkeit (STR) von Bauteilen ohne geotechnische Einwirkungen | |||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Kombination | Ständige Einwirkungen | Veränderliche Einwirkungen | |||||||||||||||||||||||||||
| Ungünstig | Günstig | Leit- einwirkung |
Begleiteinwirkung | ||||||||||||||||||||||||||
| Grundkombination | γG,j,sup · G k,j,sup | γG,j,inf · G k,j,inf | γQ,1 · Q k,1 | γQ,i · ψ0,i · Q k,i | |||||||||||||||||||||||||
| γG,j;sup = 1,35 γG,j,inf = 1,00 |
für Nachweise STR für Nachweise STR | ||||||||||||||||||||||||||||
| Haupt | Weitere | ||||||||||||||||||||||||||||
| Außergewöhnlich | G k,j,sup | G k,j,inf | Ad | (ψ1,1 oder ψ2,1) · Q k,i |
ψ2,i · Q k,i | ||||||||||||||||||||||||
| Erdbeben | G k,j,sup | G k,j,inf | γf · A Ek oder A Ed | ψ2,i · Q k,i | |||||||||||||||||||||||||
| Grenzzustände der Gebrauchstauglichkeit | |||||||||||||||||||||||||||||
| Kombination | Ständige Einwirkung | Veränderliche Einwirkungen | |||||||||||||||||||||||||||
| Ungünstig | Günstig | Dominierende | Weitere | ||||||||||||||||||||||||||
| Charakteristisch | G k,j,sup | G k,j,inf | Q k,1 | ψ0,i · Q k,i | |||||||||||||||||||||||||
| Häufig | G k,j,sup | G k,j,inf | ψ1,1 · Q k,1 | ψ2,i · Q k,i | |||||||||||||||||||||||||
| Quasi-ständig | G k,j,sup | G k,j,inf | ψ2,1 · Q k,1 | ψ2,i · Q k,i | |||||||||||||||||||||||||
| Anmerkung: Für die außergewöhnliche Bemessungssituation und Erdbeben im Grenzzustand der Tragfähigkeit, sowie Nachweise im Grenzzustand der Gebrauchstauglichkeit werden die Teilsicherheitsbeiwerte mit 1,0 berücksichtigt. | |||||||||||||||||||||||||||||
Tab. 1.1: Bemessungswerte der Einwirkungen und empfohlene Teilsicherheitsbeiwerte nach EN 1990:2003 [N 4] (Zusammenfassung)
Kombinationsbeiwerte ψ0, ψ1 und ψ2
Mit Hilfe der Kombinationsbeiwerte ψ0, ψ1 und ψ2 wird die reduzierte Wahrscheinlichkeit des gleichzeitigen Auftretens der ungünstigen Auswirkungen mehrerer unabhängiger veränderlicher Einwirkungen berücksichtigt.
Die Einwirkungen werden unterteilt in
- Charakteristischer Wert einer Einwirkung [N 4]
Der charakteristische Wert einer Einwirkung wird so gewählt, dass er während des Bezugszeitraumes nicht überschritten wird. - Seltener Wert
Der Kombinationswert einer selten auftretenden veränderlichen Einwirkung wird begleitend mit einer veränderlichen Einwirkung verwendet. - Häufiger Wert einer veränderlichen Einwirkung [N 4]
Der Kombinationswert einer häufig auftretenden veränderlichen Einwirkung wird so gewählt, dass die Überschreitungshäufigkeit innerhalb der Nutzungsdauer auf einen bestimmten Wert begrenzt bleibt. - Quasi-ständiger Wert einer veränderlichen Einwirkung [N 4]
Der Kombinationswert einer quasi-ständig auftretenden veränderlichen Einwirkung wird so gewählt, dass der Überschreitungszeitraum einen wesentlichen Teil des Bezugszeitraumes ausmacht.
| Einwirkungen | ψ0 | ψ1 | ψ2 |
|---|---|---|---|
| Nutzlasten im Hochbau a) | |||
| Kategorie A: Wohngebäude | 0,7 | 0,5 | 0,3 |
| Kategorie B: Bürogebäude | 0,7 | 0,5 | 0,3 |
| Kategorie C: Versammlungsbereiche | 0,7 | 0,7 | 0,6 |
| Kategorie D: Verkaufsflächen | 0,7 | 0,7 | 0,6 |
| Kategorie E: Lagerflächen | 1,0 | 0,9 | 0,8 |
| Kategorie F: Fahrzeugverkehr im Hochbau, Fahrzeuggewicht ≤ 30 kN | 0,7 | 0,7 | 0,6 |
| Kategorie G: Fahrzeugverkehr im Hochbau, 30 kN < Fahrzeuggewicht ≤ 160 kN | 0,7 | 0,5 | 0,3 |
| Kategorie H: Dächer | 0 | 0 | 0 |
| Schneelasten im Hochbau (siehe EN 1991-1-3)b) | |||
| Finnland, Island, Norwegen, Schweden | 0,7 | 0,5 | 0,2 |
| für Orte in CEN-Mitgliedsstaaten mit einer Seehöhe über 1.000 m ü. NN | 0,7 | 0,5 | 0,2 |
| für Orte in CEN-Mitgliedsstaaten mit einer Seehöhe niederiger als 1.000 m ü. NN | 0,5 | 0,2 | 0 |
| Windlasten im Hochbau (siehe EN 1991-1-4) c) | 0,6 | 0,2 | 0 |
| Temperaturanwendungen (ohne Brand) im Hochbau, siehe EN 1991-1-5 d) | 0,6 | 0,5 | 0 |
| Anmerkung: Die Festlegung der Kombinationsbeiwerte erfolgt im nationalen Anhang. | |||
Tab. 1.2: empfohlene Kombinationsbeiwerte nach EN 1990 [N 4]
1.4
Basisvariable
Bemessungswert der Beanspruchbarkeit (Tragfähigkeit)
Der Bemessungswert der Tragfähigkeit eines Querschnitts, Bauteils bzw. einer Verbindung wird im Holzbau mit Hilfe der Gleichung (1.9) berechnet.
| (1.9) |
| mit | ||
| Xk bzw. Rk | Charakteristischer Wert einer Festigkeitseigenschaft bzw. Beanspruchbarkeit | |
| kmod | Modifikationsbeiwert zur Berücksichtigung der Lasteinwirkungsdauer und der Nutzungsklasse, siehe Tab. 1.8 und 1.9 | |
| γM | Teilsicherheitsbeiwert einer Baustoffeigenschaft, siehe Tab. 1.6 und 1.7 |
Der Modifikationsbeiwert kmod ist ein Sicherheitsfaktor, der den Einfluss des Tragverhaltens durch unterschiedliche Feuchtegehalte und die Dauer der Lasteinwirkung berücksichtigt.
Der Sicherheitsfaktor γM ist der Teilsicherheitsbeiwert der ungünstige Streuungen von Baustoffeigenschaften, der Modellunsicherheiten und von Größenabweichungen berücksichtigt.
Einwirkungen und Umgebungseinflüsse
Klassen der Lasteinwirkungsdauer (KLED)
Die Klassifizierung der Dauer der Einwirkung auf ein Gebäude bzw. Tragwerk ist Tab. 1.3 und 1.4 zu entnehmen.
| KLED | Größenordnung der akkumulierten Lasteinwirkungsdauer |
Beispiele |
| ständig | länger als 10 Jahre | Eigenlasten von Tragwerken, Ausrüstungen, festen Einbauten und haustechnischen Anlagen |
| lang | 6 Monate bis 10 Jahre | Lagerstoffe |
| mittel | 1 Woche bis 6 Monate | Nutzlasten, Schneelasten bei Geländehöhe größer 1.000 m ü. NN |
| kurz | kürzer als eine Woche | Schneelasten bei Geländehöhen bis 1.000 m ü. NN, Windlasten |
| sehr kurz | kürzer als 1 Minute | außergewöhnliche Lasten, Anpralllasten, Erdbebenlasten |
Tab. 1.3: Zuordnung von Tragwerken in KLED nach EN 1995-1-1:2004/A1:2008 [N 1] und ÖNORM B 1995-1-1:2010 [N 3]
| Einwirkung | KLED |
| Wichten und Flächenlasten nach DIN 1055-1 | ständig |
| Lotrechte Nutzlasten nachDIN 1055-3 A Spitzböden, Wohn- und Aufenthaltsräume |
mittel mittel kurz mittel lang mittel kurz mittel kurz kurz kurz kurz |
| Horizontale Nutzlasten nach DIN 1055-3 | |
| Horizontale Nutzlasten infolge von Personen auf Brüstungen, Geländern und anderen Konstruktionen, die als Absperrung dienen |
kurz |
| Horizontallasten zur Erzielung einer ausreichenden Längs- und Queraussteifung | a |
| Horizontallasten für Hubschrauberlandeplätze auf Dachdecken - für horizontale Nutzlasten - für den Überrollschutz |
kurz sehr kurz |
| Windlasten nach DIN 1055-4 | kurz |
| Schneelasten und Eislasten nach DIN 1055-5 - Geländehöhen des Bauwerksstandortes NN ≤ 1.000 m - Geländehöhen des Bauwerksstandortes NN > 1.000 m |
kurz mittel |
| Anpralllasten nach DIN 1055-9 | sehr kurz |
| Horizontallasten aus Kran- und Maschinenbetrieb nach DIN 1055-10 | kurz |
| a entsprechend der zugehörigen Lasten | |
Tab. 1.4: Zuordnung von Tragwerken in KLED nach DIN 1055-1, DIN 1055-3, DIN 1055-4, DIN 1055-5, DIN 1055-9, DIN 1055-10 und DIN 1055-100
Nutzungsklasse (NKL)
Durch die hygroskopischen Eigenschaften des Holzes passt sich die Holzfeuchte durch Feuchtigkeitsaufnahme und Feuchtigkeitsabgabe an die Umgebungsfeuchte an. Die sich einstellende Holzgleichgewichtsfeuchte beeinflusst die technologischen Eigenschaften des Holzes (mit zunehmender Feuchtigkeit nehmen die Festigkeit und der E-Modul ab). Wegen des Umwelteinflusses auf Holzbauteile ist es notwendig, die Tragwerke in Nutzungsklassen zu unterteilen. Sie kennzeichnen die klimatischen Verhältnisse der Umgebung des Bauwerkes während seiner Lebensdauer.
| Nutz- ungs- klasse |
Umgebungsklima | Holzfeuchte der meisten Nadelhölzer |
Tragwerks- bzw. Gebäudetyp | |
| Temperatur | relative Luft- feuchte a | |||
| 1 | 20 °C | ≤ 65% | ≤ 12% | Innenräume von Wohn-, Schul- und Verwaltungsbauten |
| 2 | 20 °C | ≤ 85% | ≤ 20% | Innenräume von Nutzbauten wie Lagerhallen, Reithallen und Industriehallen sowie überdachte Konstruktionen im Freien, deren Bauteile nicht der freien Bewitterung ausgesetzt sind (30° Regeneinfallswinkel) |
| 3 | - | - | > 20% | Bauteile im Freien mit konstruktivem Holzschutz |
| a Die relative Luftfeuchte darf in den Nutzungsklassen 1 und 2 maximal für einige Wochen im Jahr die angegebenen Werte übersteigen. | ||||
Tab. 1.5: Zuordnung von Tragwerken in Nutzungsklassen nach ÖNORM B 1995-1-1 [N 3] und DIN 1052:2008 [N 2]
Zur Verminderung von Schwindrissen und Maßänderungen sollten die verwendeten Holzbauteile für die Nutzungsklassen 1 und 2 mit einer Einbaufeuchte u ≤ 20 %, und für die Nutzungsklasse 3 mit u ≤ 25 % begrenzt werden (lt. DIN 1052:2008 [N 2] ).
Teilsicherheitsbeiwerte für Baustoffeigenschaften und Widerstände
Tab. 1.6: Empfohlene Teilsicherheitsbeiwerte für |
Tab. 1.7: Empfohlene Teilsicherheitsbeiwerte für | ||||||||||||||||||||||||||||||
1.5
Baustoffeigenschaften
Modifikationsbeiwerte der Festigkeiten zur Berücksichtigung der Nutzungsklasse und Lasteinwirkungsdauer
Anmerkungen aus EN 1995-1-1:2004/A1:2008 [N 1] und DIN 1052:2008 [N 2] :
Setzt sich eine Lastkombination aus unterschiedlichen Lasteinwirkungsdauern zusammen, ist in der Regel der Wert für kmod mit der kürzeren Dauer zu verwenden.
Anmerkungen aus EN 1995-1-1:2004/A1:2008 [N 1] :
Besteht eine Verbindung aus Holzteilen mit unterschiedlichen zeitabhängigem Verhalten, so ist kmod mit kmod,1 und kmod,2 der beiden Holzteile mittels zu ermitteln.
| Baustoff (Bezugsnorm) | Nutzungsklasse | Baustoff (Bezugsnorm) | Nutzungsklasse | ||||
| Vollholz (EN 14081-1) Brettschichtholz (EN 14080) Furnierschichtholz (EN 14374, EN 14279) Sperrholz (EN 636-1, -2, -3) |
OSB/2a (EN 300) Spanplatten Typ P4a, P5 (EN 312) Holzfaserplatten, hart: HB.LAa, HB.LA1, HB.LA2 (EN 622-2) | ||||||
| Lasteinwirkungsdauer | 1 | 2 | 3 | Lasteinwirkungsdauer | 1 | 2 | |
| ständig | 0,60 | 0,60 | 0,50 | ständig | 0,30 | 0,20 | |
| lang | 0,70 | 0,70 | 0,55 | lang | 0,45 | 0,30 | |
| mittel | 0,80 | 0,80 | 0,65 | mittel | 0,65 | 0,45 | |
| kurz | 0,90 | 0,90 | 0,70 | kurz | 0,85 | 0,60 | |
| sehr kurz | 1,10 | 1,10 | 0,90 | sehr kurz | 1,10 | 0,80 | |
| Baustoff (Bezugsnorm) | Nutzungsklasse | Baustoff (Bezugsnorm) | Nutzungsklasse | ||||
| OSB/3, OSB/4 (EN 300) Spanplatten Typ P6a, P7 (EN 312) |
Holzfaserplatten, mittelhart: MBH.LA1a, MBH.LA2a (EN 622-3) MBH.HLS1, MBH.HLS2 (EN 622-3) Holzfaserplatten, MDF: MDF.LAa, MDF.HLS (EN 622-5) | ||||||
| Lasteinwirkungsdauer | 1 | 2 | 3 | Lasteinwirkungsdauer | 1 | 2 | |
| ständig | 0,40 | 0,30 | - | ständig | 0,20 | - | |
| lang | 0,50 | 0,40 | - | lang | 0,40 | - | |
| mittel | 0,70 | 0,55 | - | mittel | 0,60 | - | |
| kurz | 0,90 | 0,70 | - | kurz | 0,80 | 0,45 | |
| sehr kurz | 1,10 | 0,90 | - | sehr kurz | 1,10 | 0,80 | |
| a Anwendungen nur für Nutzungsklasse 1 erlaubt | |||||||
Tab. 1.8: Empfohlene Modifikationsbeiwerte kmod nach EN 1995-1-1:2004/A1:2008
| Baustoff | Nutzungsklasse | Baustoff (Bezugsnorm) | Nutzungsklasse | ||||
| Vollholz, Brettschichtholz Balkenschichtholz, Furnierschichtholz Brettsperrholz, Sperrholz |
Kunstharzgebundene Spanplatten Zementgebundene Spanplatten Faserplatten, Typ HB.HLA2 (DIN EN 622-2:2004-07) | ||||||
| Lasteinwirkungsdauer | 1 | 2 | 3 | Lasteinwirkungsdauer | 1 | 2 | |
| ständig | 0,60 | 0,60 | 0,50 | ständig | 0,30 | 0,20 | |
| lang | 0,70 | 0,70 | 0,55 | lang | 0,45 | 0,30 | |
| mittel | 0,80 | 0,80 | 0,65 | mittel | 0,65 | 0,45 | |
| kurz | 0,90 | 0,90 | 0,70 | kurz | 0,85 | 0,60 | |
| sehr kurz | 1,10 | 1,10 | 0,90 | sehr kurz | 1,10 | 0,80 | |
| Baustoff (Bezugsnorm) | Nutzungsklasse | Baustoff (Bezugsnorm) | Nutzungsklasse | ||||
| OSB-Platten, Typen OSB/2a, OSB/3 und OSB/4 (DIN EN 300:2006-09) |
Faserplattena, Typ MBH.LA2 (DIN EN 622-3:2004-07) Gipskartonplatten, Typen GKBa, GKFa, GKBI und GKFI (DIN 18180) | ||||||
| Lasteinwirkungsdauer | 1 | 2 | 3 | Lasteinwirkungsdauer | 1 | 2 | |
| ständig | 0,40 | 0,30 | - | ständig | 0,20 | 0,15 | |
| lang | 0,50 | 0,40 | - | lang | 0,40 | 0,30 | |
| mittel | 0,70 | 0,55 | - | mittel | 0,60 | 0,45 | |
| kurz | 0,90 | 0,70 | - | kurz | 0,80 | 0,60 | |
| sehr kurz | 1,10 | 0,90 | - | sehr kurz | 1,10 | 0,80 | |
| a nur Nutzungsklasse 1 | |||||||
Tab. 1.9: Empfohlene Modifikationsbeiwerte kmod nach DIN 1052:2008
| Baustoff (Bezugsnorm) | Nutzungsklasse | Baustoff (Bezugsnorm) | Nutzungsklasse | ||||
| 1 | 2 | 3 | 1 | 2 | |||
| Vollholz (EN 14081-1) Brettschichtholz (EN 14080) Furnierschichtholz (EN 14374, EN 14279) |
0,60 | 0,80 | 2,00 | OSB/21 (EN 300) Spanplatten, Typ P41, Typ P5 (EN 312) Holzfaserplatten, hart: HB.LA1, HB.LA1, HB.LA2 (EN 622-2) Holzfaserplatten, MDF: MDF.LA1, MDF.HLS (EN 622-5) |
2,25 | 3,00 | |
| Sperrholz (EN 636-11, -22,-3) |
0,80 | 1,00 | 2,50 | ||||
| OSB/3, OSB/4 (EN 300) |
1,50 | 2,25 | - | Holzfaserplatten, mittelhart: MBH.LA11, MBH.LA2,1 MBH.HLS1, MBH.HLS2 (EN 622-3) |
3,00 | 4,00 | |
| Spanplatten, Typ P61, P7 (EN 312) | |||||||
| 1 Verwendung nur in Nutzungsklasse 1 2 Verwendung nur in Nutzungsklasse 1 und 2 | |||||||
| Anmerkung: Universalkeilzinkenverbindungen nach EN 387 bei denen sich in Verbindungen die Faserrichtung verändert dürfen nicht in Nutzungsklasse 3 verwendet werden. | |||||||
Tab. 1.10: Empfohlene Verformungsbeiwert kdef nach EN 1995-1-1:2004/A1:2008
Anmerkung zu EN 1995-1-1:2004/A1:2008 [N 1] :
Besteht eine Verbindung aus Holzbauteilen mit dem gleichen zeitabhängigen Verhalten, so ist der Wert von kdef zu verdoppeln. Wenn eine Verbindung aus Holz- und/oder Holzwerkstoffen mit unterschiedlichem zeitabhängigen Verhalten besteht, ist in der Regel der Wert für kdef mit den Verformungsbeiwerten kdef,1 und kdef,2 der beteiligten Holzbaustoffe mittels zu berechnen.
| Baustoff | Nutzungsklasse | Baustoff (Bezugsnorm) | Nutzungsklasse | ||||
| 1 | 2 | 3 | 1 | 2 | |||
| Vollholza Brettschichtholz Furnierschichtholzb Balkenschichtholz Brettsperrholz |
0,60 | 0,80 | 2,00 | Kunstharzgebundene Spanplatte |
2,25 | 3,00 | |
| Zementgebundene Spanplatten | |||||||
| Faserplatten, Typ HB.LA2 (DIN EN 622-2:2004-07) | |||||||
| Sperrholz | 0,80 | 1,00 | 2,50 | Faserplatten, Typ MBH.LA2 (DIN EN 622-3:2004-07) |
3,00 | 4,00 | |
| Furnierschichtholzc | |||||||
| OSB-Platten | 1,50 | 2,25 | - | Gipskartonplatten | |||
| a Die Werte für kdef für Vollholz, dessen Feuchte beim Einbau im Fasersättigungsbereich oder darüber liegt und im eingebauten Zustand austrocknen kann, sind um 1,0 zu erhöhen. b mit allen Furnieren faserparallel | |||||||
Tab. 1.11: Empfohlener Verformungsbeiwert kdef nach DIN 1052:2008
Anmerkung zu DIN 1052:2008 [N 2]
Ist der ständige Lastanteil > 70 % der Gesamtlast soll die Steifigkeit druckbeanspruchter Bauteile um den Faktor 1 / (1+kdef) abgemindert werden. Bei Tragwerken aus Bauteilen mit unterschiedlichen zeitabhängigen Verformungsverhalten sollen die Steifigkeiten der einzelnen Bauteile um den Faktor 1 / (1+kdef) abgemindert werden.
Besteht eine Verbindung aus Holzbaustoffen mit unterschiedlichen kdef-Werten, ist das arithmetische Mittel zu verwenden. Bei Stahlblech-Holz-Verbindungen ist der Verformungsbeiwert des Holzes zu verwenden.
Baustoffkennwerte
Baustoffeigenschaften werden durch charakteristische Werte angegeben, die einem angenommenen Quantilwert einer statistischen Verteilung entsprechen. In der Regel sind das die
- 5 %-Quantilwerte bei Festigkeiten und Rohdichten, und
- 5 %-Quantilwerte oder Mittelwerte bei Steifigkeiten.
Vollholz
- Dieser Abschnitt ist ausgelagert, siehe: Vollholz
Brettschichtholz
- Dieser Abschnitt ist ausgelagert, siehe: Brettschichtholz
1.6
Nachweise im Grenzzustand der Tragfähigkeit
Allgemeines
Im Zuge der Nachweisführung für Tragwerke / Bauwerke sind nach EN 1990 (6.4.1) folgende Nachweise zu erfüllen:
- EQU (engl.: equilibrium)
Verlust der Lagesicherheit des Tragwerks oder eines seiner Teile, die als Starrkörper betrachtet werden dürfen [2]
| (1.10) |
- STR (engl.: structural failure)
Versagen oder übermäßige Verformungen des gesamten Tragwerks oder von Tragwerksteilen, wobei die Tragfähigkeit von Bauteilen und deren Festigkeit maßgebend wird (Stabilität) [2]
| (1.11) |
- GEO (engl.: geotechnic)
Versagen oder übermäßige Verformungen des Baugrundes [2]
| (1.12) |
- FAT (engl.: fatique)
Ermüdungsversagen des gesamten Tragwerks oder von Tragwerksteilen [2]
| mit | ||
| Ed,dst | Bemessungswerte der Auswirkungen der destabilisierenden Einwirkungen | |
| Rd,stb | Bemessungswerte der Auswirkungen der stabilisierenden Einwirkungen | |
| Ed | Bemessungswerte der Auswirkungen der Einwirkungen | |
| Rd | Bemessungswerte der zugehörigen Tragfähigkeiten |
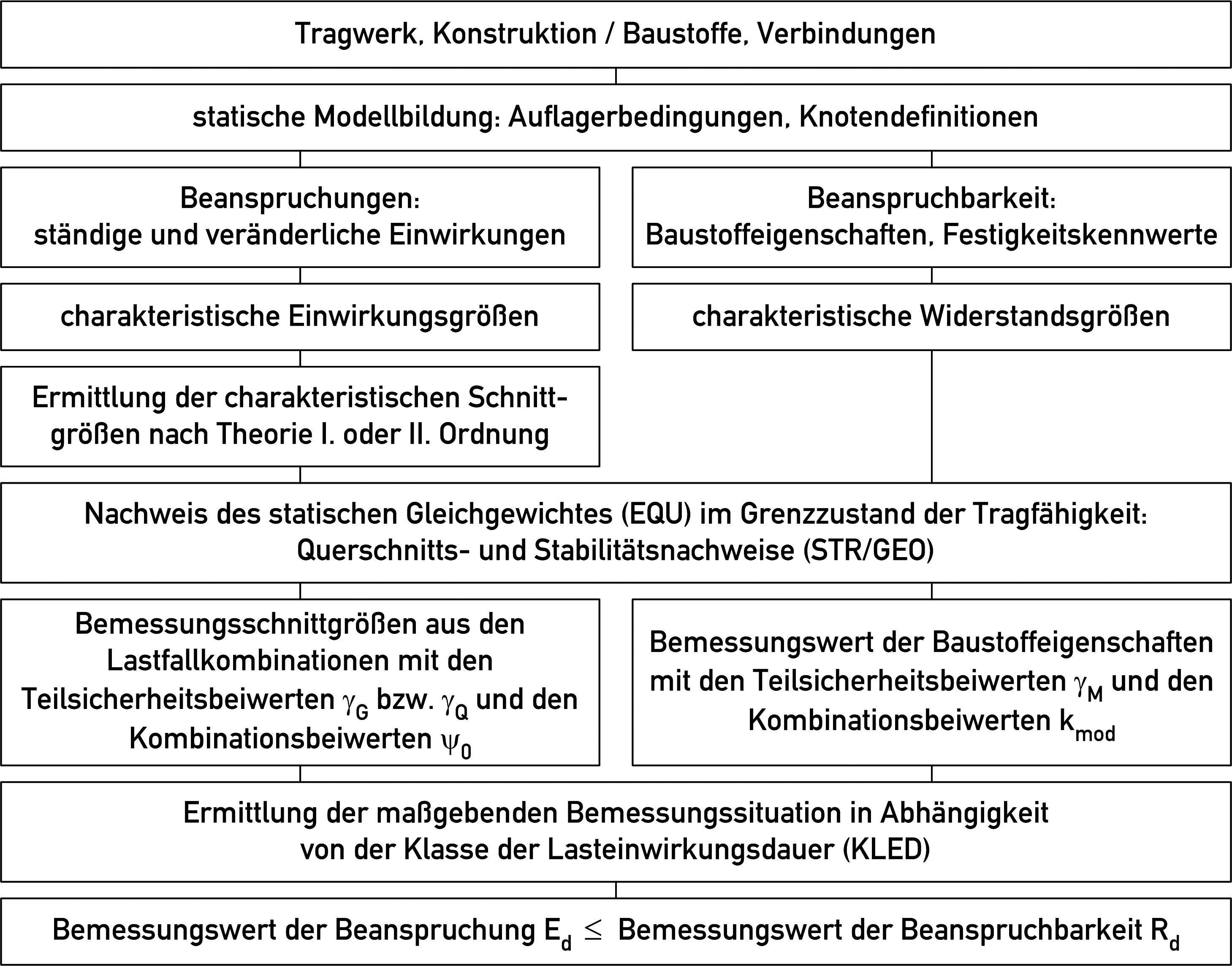
Die Nachweise der Grenzzustände der Tragfähigkeiten können einerseits über die Spannungszustände
| (1.13) |
oder durch den Vergleich der einwirkenden Schnittgrößen mit den Widerständen auf der Baustoffseite
| (1.14) |
geführt werden.
Abb. 1.5 : Ablaufschema beim Nachweis der Grenzzustände der Tragfähigkeit von Bauteilen
Querschnittsnachweise nach OENORM B 1995 [N 3] und DIN 1052 [N 2]
Zug in Faserrichtung
Aus den charakteristischen Werten der ständigen Einwirkungen Gk und der veränderlichen Einwirkungen Qk erhält man nach Ermittlung der maßgebenden Lastkombination den Bemessungswert der Zugbeanspruchung st,0,d. Diesem wird der Bemessungswert der Zugfestigkeit ft,0,d gegenübergestellt. Bei der Bemessung der Querschnittstragfähigkeit sind evtl. vorhandene Querschnittsschwächungen zu berücksichtigen
(ANetto ~ 0,3 · ABrutto bis 0,8 · ABrutto (abhängig von derVerbindungsart)).
Die Spannungen müssen die folgende Bedingung erfüllen:
| (1.15) |
| mit | ||
| Bemessungswert der Zugspannung | ||
| Bemessungswert der Zugfestigkeit |
Druck in Faserrichtung des Holzes
Die Bemessungswerte für Druck in Faserrichtung σc,0,d aus der maßgebenden Lastkombination sind den Bemessungswerten der Druckfestigkeit fc,0,d gegenüber zustellen.
Die Spannungen müssen die folgende Bedingung erfüllen:
| (1.16) |
| mit | ||
| Bemessungswert der Druckspannung | ||
| Bemessungswert der Druckfestigkeit |
Druck rechtwinklig zur Faserrichtung des Holzes
Durch die anisotropen Eigenschaften hat Holz bei Beanspruchung in den verschiedenen Richtungen auch unterschiedliche Eigenschaften. Weiters ist die Beanspruchbarkeit bzw. das Verformungsverhalten bei Bauteilen ohne einen Überstand der Hirnholzflächen im Bereich der Lasteinleitung schlechter, als bei Beanspruchungen mit über den Lasteinleitungsbereichen überstehenden Holzfasern.
Wird ein Holzprobekörper vollflächig belastet, verhalten sich die Holzfasern wie übereinander gestapelte Rohre die im plastischen Bereich zusammengequetscht werden [4]. Wird stattdessen nur eine Teilflächenbelastung aufgebracht, ergibt sich eine höhere Steifigkeit. Eine Begründung dieser Tatsache kann durch den sogenannten „Einhängeeffekt“, der über die Lasteinleitungslänge hinauslaufenden Fasern resultiert, gefunden werden [5].
| Baustoff | l1 ≥ 2 · h | l1 < 2 · h | |
| Art der Lasteinleitung | |||
| kontinuierliche Unterstützung |
punktuelle Unterstützung |
||
| Vollholz aus Nadelholz | 1,25 | 1,50 | 1,00 |
| Brettschichtholz aus Nadelholz | 1,50 | 1,75 a | 1,00 |
| a Vorausgesetzt es gilt: l ≤ 400 mm, ansonsten darf l = 400 mm oder kc,90 = 1,00 angenommen werden. | |||
| Es bedeuten: l ...... Kontaktlänge | |||
Tab. 1.14: Querdruckbeiwert kc,90 nach EN 1995-1-1:2004/A1:2008 und DIN 1052:2008
Die Spannungen müssen die folgende Bedingung erfüllen:
| (1.17) |
| mit | ||
| Bemessungswert der Querdruckspannung | ||
| Bemessungswert der Querdruckfestigkeit | ||
| Querdruckbeiwert siehe Tab. 1.14 |
Für die effektive Druckfläche Aef rechtwinklig zur Faserrichtung des Holzes, darf die tatsächliche Kontaktlänge durch den Einhängeeffekt parallel zur Faserrichtung um bis zu 30 mm je Seite verlängert werden.
Druck unter einem Winkel zur Faserrichtung des Holzes
Für 0° < α < 90° sind die folgenden Nachweise zu führen:
Nachweis nach EN 1995-1-1:2004/A1:2008 [N 1]
| (1.18) |
Nachweis nach DIN 1052:2008 [N 2]
| (1.19) |
| (1.20) |
| (1.21) |
| mit | ||
| Bemessungswert der Druckspannung | ||
| α | Winkel zwischen der Beanspruchungsrichtung und Faserrichtung des Holzes | |
| kc,90 | Querdruckbeiwert siehe Tab. 1.14 |
Biegung
Träger mit entsprechenden Abmessungen und Auflagerausbildungen bei denen die Gefahr des Biegedrillknickens ausgeschlossen werden kann, dürfen die Biegespannungen nach der linearen Elastizitätstheorie ermittelt werden. Für kippgefährdete Balken sind zusätzlich Stabilitätsnachweise gegen Biegedrillknicken zu führen.
Anmerkung:
Zur Berücksichtigung der Spannungsverteilungen durch die Inhomogenitäten des Baustoffes wird in EN 1995-1-1:2004/A1:2008 der Beiwert km verwendet. In der DIN 1052:2008 wird der Beiwert zur Berücksichtigung der Inhomogenitäten mit kred bezeichnet, während der Beiwert km als Kippbeiwert Verwendung findet.
Die Spannungen müssen die folgende Bedingung erfüllen:
| (1.22) |
| (1.23) |
| mit | ||
| Bemessungswert der Biegespannung für Rechteckquerschnitte | ||
| km = 0,7 | Beiwert für Rechteckquerschnitte aus Vollholz, BSH und Furnierschichtholz (Anmerkung: In der DIN 1052:2008 muss h/b ≤ 4 eingehalten werden) | |
| km = 1,0 | Beiwert für andere Querschnitte |
Biegung und Zug
Bei einer kombinierten Beanspruchung aus Biegung und Zug müssen die folgenden Bedingungen nach Gleichung (1.24) und (1.25) erfüllt sein
| (1.24) |
| (1.25) |
| mit | ||
| km | Angaben gemäß 1.6.2.5 Biegung |
Biegung und Druck
Bei einer kombinierten Beanspruchung aus Biegung und Druck müssen die folgenden Bedingungen erfüllt sein:
| (1.26) |
| (1.27) |
| mit | ||
| km | Angaben gemäß 1.6.2.5 Biegung |
Schub aus Querkraft
Bei Schub und Rollschub muss die Gleichung (1.28) erfüllt sein:
| (1.28) |
| mit | ||
| Bemessungswert der mittleren Schubspannungen bei Rechteckquerschnitten |
Für den Nachweis der Beanspruchbarkeit auf Schub biegebeanspruchter Bauteile, sollte der Einfluss von möglichen Rissen nach EN 1995-1-1:2004/A1:2008 durch eine Abminderung der Querschnittsbreite mit dem Faktor kcr erfolgen. Dieser Faktor ist in den Schubfestigkeitswerten von DIN 1052:2008 [N 2] bereits enthalten.
| mit | ||
| kcr = 0,67 | für Vollholz | |
| kcr = 0,671) | für Brettschichtholz | |
| kcr = 1,00 | für für andere holzbasierte Produkte nach EN 13986 und EN 14374 |
1) Gemäß ÖNORM B 1995-1-1 [N 3] ist in der Nachweisführung für alle Brettschichtholzfestigkeitsklassen ein Rissefaktor kcr = 0,83 , verbunden mit der Berücksichtigung eines konstanten charakteristischen Schubfestigkeitswertes von fv,k = 3,0 N/mm², zu verwenden.
Nach der DIN 1052:2008 [N 2] soll bei einer Beanspruchung durch Doppelbiegung von Rechteckquerschnitten die folgende Bedingung eingehalten werden:
| (1.29) |
Anmerkung:
In der EN 1995-1-1 sind zu dieser Beanspruchungsart bzw. einer Nachweisführung keine Angaben zu finden.
Torsion
Bei auf Torsion beanspruchten Querschnitten dürfen die Torsionsspannungen wie für Bauteile aus isotropem Material berechnet werden.
Für den Nachweis nach DIN 1052:2008 [N 2] muss die Gleichung (1.30) erfüllt werden
| (1.30) |
Für den Nachweis nach EN 1995-1-1:2004/A1:2008 [N 1]gilt Gleichung (1.31)
| (1.31) |
mit
| (1.32) |
| τtor,d | Bemessungswert der Torsionsspannungen | |
| fv,d | Bemessungswert der Schubfestigkeit | |
| kshape | Beiwert zur Berücksichtigung der Querschnittsform | |
| h | die größere Querschnittsabmessung | |
| b | die kleinere Querschnittsabmessung |
Schub aus Querkraft und Torsion
Nach DIN 1052:2008 [N 2] muss die Bedingung nach Gleichung (1.33)
| (1.33) |
erfüllt werden.
Anmerkung:
In der EN 1995-1-1:2004/A1:2008 sind keine Angaben zu dieser Beanspruchungsart zu finden.
Bauteilnachweise (Stabilitätsnachweise)
Allgemeines
Druckbeanspruchte Bauteile können vor Erreichen ihrer Querschnittstragfähigkeit instabil werden und infolge übergroßer Verformungen ihre Tragfähigkeit verlieren, weshalb diese entsprechend zu dimensionieren bzw. nachzuweisen sind.
Im Folgenden wird die Nachweisführung nach DIN 1052:2008 [N 2] für Druckstäbe nach dem sog. „Ersatzstabverfahren“ dargestellt. Für die Nachweisführung nach EN 1995-1-1:2004/A1:2008 [N 1] wird auf die Festlegungen des Abschnittes 6.3 der genannten Norm verwiesen.
Druckstäbe mit planmäßig mittigem Druck
Die folgende Bedingung muss erfüllt sein
| (1.34) |
Der Knickbeiwert kc beträgt
mit
| (1.35) |
und
| (1.36) |
| βc = 0,2 | für Vollholz und Balkenschichtholz, | |
| βc = 0,1 | für Brettschichtholz und Holzwerkstoffe |
mit dem bezogenen Schlankheitsgrad
| (1.37) |
| Dabei ist: | ||
| σc,crit | kritische Druckspannung, berechnet mit den 5%-Quantilen der Steifigkeitskennwerte | |
| λ = lef / i | Schlankheitsgrad | |
| i | Trägheitsradius | |
| lef = β · s oder β · h | Ersatzstablänge | |
| β | Knicklängenbeiwert | |
| s bzw. h | Stablänge |
Biegestäbe ohne Druckkraft
Biegestäbe müssen an den Auflagern gegen Verdrehen gesichert sein.
Die folgende Bedingung muss erfüllt sein
| (1.38) |
Der Kippbeiwert km beträgt
| (1.39) |
mit dem bezogenen Kippschlankheitsgrad
| (1.40) |
| Dabei ist: | ||
| σc,crit | kritische Biegedruckspannung, berechnet mit dem 5%-Quantilwerten der Steifigkeitswerte | |
| mit | Jz Jt Wy |
Flächenmoment 2. Grades um die z-Achse, Torsionsträgheitsmoment Widerstandsmoment |
Für Biegestäbe mit einem Rechteckquerschnitt der Breite b und der Höhe h darf der bezogene Kippschlankheitsgrad berechnet werden zu
| (1.41) |
Bei Biegestäben aus Brettschichtholz darf zur Berechnung des bezogenen Kippschlankheitsgrades λrel,m bzw. der kritischen Biegedruckspannung σm,crit das Produkt der 5%-Quantilen der Steifigkeitskennwerte mit dem Faktor 1,4 multipliziert werden.
Für den gabelgelagerten Einfeldträger mit konstantem Moment entspricht die Ersatzlänge lef der Stützweite l des Trägers.
Für andere Lagerungen und andere Einwirkungen ist die Ersatzstablänge lef nach Anhang E von DIN 1052:2008 [N 2] zu berechnen.
Für Biegestäbe, bei denen eine seitliche Verschiebung des gedrückten Randesüber die ganze Länge verhindert wird, darf km = 1 gesetzt werden.
Für Biegestäbe mit Rechteckquerschnitt und darf km = 1 gesetzt werden. Dabei ist b die Trägerbreite.
Stäbe mit Biegung und Druck
Die folgenden Bedingungen müssen erfüllt sein:
| (1.42) |
und
| (1.43) |
| Dabei ist | ||
| kc,y | Knickbeiwert nach Glg. 1.35 für Knicken um die y-Achse | |
| kc,z | Knickbeiwert nach Glg. 1.35 für Knicken um die z-Achse | |
| km | Kippbeiwert nach Glg. 1.39 | |
| kred | Beiwert nach Abschnitt 1.6.2.5 - Biegung |
Stäbe mit Biegung und Zug
Die folgenden Bedingungen müssen erfüllt sein:
| (1.44) |
und
| (1.45) |
| Dabei ist | ||
| km | Kippbeiwert nach Glg. 1.39 | |
| kred | Beiwert nach Abschnitt 1.6.2.5 - Biegung |
1.7
Nachweise im Grenzzustand der Gebrauchstauglichkeit
Grenzwerte für die Durchbiegung von Biegestäben
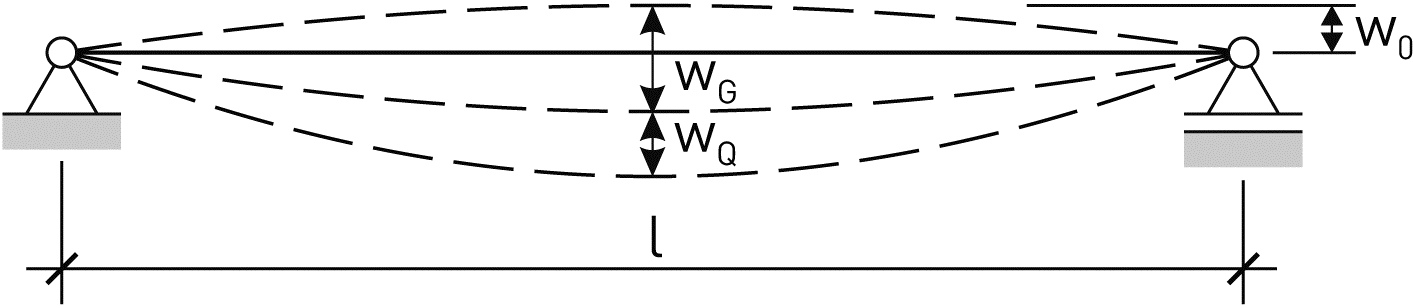
Die zulässigen Verformungen bzw. Durchbiegungen von Tragwerken sollen mit der vorgesehenen Nutzung abgestimmt werden. In Tab. 1.15 werden Empfehlungen für die zulässigen Durchbiegungen von Biegeträgern gegeben.
| Rechenwerte der Durchbiegungen | Grenzwerte der Durchbiegungen | ||
| Biegeträger | Kragträger | ||
| Charakteristische Bemessungs- situation |
wQ,inst | l / 300 | lk / 150 |
| wfin - wQ,inst | l / 200 | lk / 100 | |
| quasi-ständige Bemessungs- situation |
wfin - w0a) | l / 200 | lk / 100 |
| a) In der ÖNORM B 1995-1-1 werden die Grenzwerte mit l/250 bzw. lk/125 angegeben. | |||
Tab. 1.15: Empfohlene Grenzwerte von Durchbiegungen nach ÖNORM B 1995-1-1:2010 [N 3] und DIN 1052:2008 [N 2]
| Es bedeuten: | ||
| wG | Durchbiegung im Fall ständiger Einwirkung | |
| wQ | Durchbiegung im Fall veränderlicher Einwirkungen | |
| w0 | Überhöhung (falls vorhanden) |
Abb. 1.6: Anteile der Durchbiegungen
Zur Berücksichtigung der Kriechverformungen wird der Faktor kdef nach Tab. 1.10 bzw. Tab. 1.11 zu verwenden.
Nachweise im Grenzzustand der Gebrauchstauglichkeit
Die Ermittlung der Durchbiegungen kann nach DIN 1052:2008 [N 2] mit den folgenden Gleichungen durchgeführt werden:
1) Gleichung für die Ermittlung der Endverformung wG,fin infolge der ständigen Einwirkungen
| (1.46) |
2) Gleichungen für die Ermittlung der Endverformung wQ,fin infolge der veränderlichen Einwirkungen
(a) für die charakteristische (seltene) Bemessungssituation
- - vorherrschende veränderliche Einwirkung
| (1.47) |
- - weitere veränderliche Einwirkungen
| (1.48) |
(b) für die quasi-ständige Bemessungssituation
- - alle veränderlichen Einwirkungen
| (1.49) |
Für Schwingungsnachweise von Wohnungsdecken sind die Angaben in Abschnitt 9.3 in DIN 1052:2008 [N 2] bzw. Abschnitt 7.3 der EN 1995-1-1:2004/A1:2008 [N 1] sowie die Angaben im nationalen Anhang 5.7 der ÖNORM B 1995-1-1:2010 [N 3] zu beachten.
Einzelnachweise
- ↑ 1,0 1,1 1,2 1,3 1,4 Blaß, H.-J.; Görlacher, R.; Steck, G.; Informationsdienst Holz, Holzbauwerke STEP1, Arbeitsgemeinschaft Holz e.V., Düsseldorf 1995
- ↑ 2,0 2,1 2,2 2,3 2,4 2,5 Augustin, M.: EUROCODE Seminar - 2009, Technische Universität Graz
- ↑ 3,0 3,1 Schueller, G.I.; Goller, B.; Modellunsicherheiten im semiprobabilistischen Sicherheitskonzept, IfM - Publikation 2 - 446
- ↑ Kelletshofer, W.; Erweiterung der vorhandenen Zulassung Z-9.1-558; Verbinder SHERPA als Holzverbindungsmittel; Haupt-Neben-Träger-Verbindungen mit „weiteren neuen“ SHERPA-Verbindern der Vinzenz Harrer GmbH; Untersuchungen zum Tragverhalten der Verbindungen, Untersuchungsbericht Nr. 7400631/09-1, Technische Universität München, Institut für Baustoffe und Konstruktion, München, 2009
- ↑ Pirnbacher, G.; Brandner, R.; Schickhofer, G.; Base Parameters of Self-Tapping Screws, Tagungsband CIB/W18, Paper 42-7-1, 17 Seiten, 2009
Normen
- ↑ 1,0 1,1 1,2 1,3 1,4 1,5 1,6 1,7 1,8 1,9 ÖNORM EN 1995-1-1:2009, Eurocode 5: Bemessung und Konstruktion von Holzbauten; Teil 1-1: Allgemeines - Allgemeine Regeln und Regeln für den Hochbau, Österreichisches Normungsinstitut (ON), Wien, 2009
- ↑ 2,00 2,01 2,02 2,03 2,04 2,05 2,06 2,07 2,08 2,09 2,10 2,11 2,12 2,13 2,14 2,15 2,16 2,17 DIN 1052:2008, Entwurf, Berechnung und Bemessung von Holzbauwerken – Allgemeine Bemessungsregeln und Bemessungsregeln für den Hochbau, DIN Deutsches Institut für Normung e. V., Berlin, 2008
- ↑ 3,0 3,1 3,2 3,3 3,4 3,5 3,6 ÖNORM B 1995-1-1:2010, Eurocode 5: Bemessung und Konstruktion von Holzbauten; Teil 1-1: Allgemeines – Allgemeine Regeln und Regeln für den Hochbau; Nationale Festlegungen, nationale Erläuterungen und nationale Ergänzungen zur ÖNORM EN 1995-1-1, Österreichisches Normungsinstitut (ON), Wien, 2010
- ↑ 4,00 4,01 4,02 4,03 4,04 4,05 4,06 4,07 4,08 4,09 4,10 4,11 4,12 4,13 4,14 4,15 4,16 4,17 4,18 4,19 ÖNORM EN 1990:2003, Eurocode; Grundlagen der Tragwerkslehre, Österreichisches Normungsinstitut (ON), Wien, 2003
Autoren / Literaturangabe
Augustin, M.; Burböck, H.; Flatscher, G.; Maderebner, R.; Salzer, R.; Schickhofer, G;
Holzbau Verbindungen
Publikation der Vinzenz Harrer GmbH, 2010















































![{\displaystyle {\mathsf {k=0{,}5\cdot \left[1+\beta _{c}\cdot \left(\lambda _{rel,c}-0{,}3\right)+\lambda _{rel,c}^{2}\right]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d5072ddfdf0afc49309e426f1eef2da8e698a61c)